Solution
# Imports
import numpy as np
import matplotlib.pyplot as plt
from datetime import datetime
import json
import copy
# Main qiskit imports
from qiskit import QuantumRegister, ClassicalRegister
from qiskit import QuantumCircuit, execute, Aer, IBMQ
# Error mitigation
from qiskit.ignis.mitigation.measurement import (complete_meas_cal,
CompleteMeasFitter,
MeasurementFilter)
# Utility functions
from qiskit.tools.jupyter import *
from qiskit.tools.monitor import job_monitor
from qiskit.providers.jobstatus import JobStatus
# We use ibmqx2
IBMQ.load_account()
backend = IBMQ.get_provider(hub='ibm-q', group='open', project='main').get_backend('ibmqx2')
# Local simulator
simulator = Aer.get_backend('qasm_simulator')
def zz_pump(q, c, p, system, ancilla):
"""Returns a QuantumCircuit implementing the ZZ pump channel on the system qubits
Args:
q (QuantumRegister): the register to use for the circuit
c (ClassicalRegister): the register to use for the measurement of the system qubits
p (float): the efficiency for the channel, between 0 and 1
system (list): list of indices for the system qubits
ancilla (int): index for the ancillary qubit
Returns:
A QuantumCircuit object
"""
zz = QuantumCircuit(q, c)
theta = 2 * np.arcsin(np.sqrt(p))
# Map information to ancilla
zz.cx(q[system[0]], q[system[1]])
zz.x(q[ancilla])
zz.cx(q[system][1], q[ancilla])
# Conditional rotation
zz.cu3(theta, 0.0, 0.0, q[ancilla], q[system[1]])
# Inverse mapping
zz.cx(q[system[1]], q[ancilla])
# Measurement
zz.h(q[system[0]])
zz.measure(q[system[0]], c[0])
zz.measure(q[system[1]], c[1])
return zz
def xx_pump(q, c, p, system, ancilla):
"""Returns a QuantumCircuit implementing the XX pump channel on the system qubits
Args:
q (QuantumRegister): the register to use for the circuit
c (ClassicalRegister): the register to use for the measurement of the system qubits
p (float): the efficiency for the channel, between 0 and 1
system (list): list of indices for the system qubits
ancilla (int): index for the ancillary qubit
Returns:
A QuantumCircuit object
"""
xx = QuantumCircuit(q, c)
theta = 2 * np.arcsin(np.sqrt(p))
# Map information to ancilla
xx.cx(q[system[0]], q[system[1]])
xx.h(q[system[0]])
xx.x(q[ancilla])
xx.cx(q[system[0]], q[ancilla])
# Conditional rotation
xx.cu3(theta, 0.0, 0.0, q[ancilla], q[system[0]])
# Inverse mapping
xx.cx(q[system[0]], q[ancilla])
# Measurement
xx.measure(q[system[0]], c[0])
xx.measure(q[system[1]], c[1])
return xx
def zz_xx_pump(q, c, p, system, ancillae):
"""Returns a QuantumCircuit implementing the composition channel on the system qubits
Args:
q (QuantumRegister): the register to use for the circuit
c (ClassicalRegister): the register to use for the measurement of the system qubits
p (float): the efficiency for both channels, between 0 and 1
system (list): list of indices for the system qubits
ancillae (list): list of indices for the ancillary qubits
Returns:
A QuantumCircuit object
"""
zx = QuantumCircuit(q, c)
theta = 2 * np.arcsin(np.sqrt(p))
# ZZ pump
## Map information to ancilla
zx.cx(q[system[0]], q[system[1]])
zx.x(q[ancillae[0]])
zx.cx(q[system[1]], q[ancillae[0]])
## Conditional rotation
zx.cu3(theta, 0.0, 0.0, q[ancillae[0]], q[system[1]])
## Inverse mapping
zx.cx(q[system[1]], q[ancillae[0]])
# XX pump
## Map information to ancilla
zx.h(q[system[0]])
zx.x(q[ancillae[1]])
zx.cx(q[system[0]], q[ancillae[1]])
## Conditional rotation
zx.cu3(theta, 0.0, 0.0, q[ancillae[1]], q[system[0]])
## Inverse mapping
zx.cx(q[system[0]], q[ancillae[1]])
# Measurement
zx.measure(q[system[0]], c[0])
zx.measure(q[system[1]], c[1])
return zx
For convenience, we define a function returning the four initial state preparations
def initial_conditions(q, system):
"""Returns a dictionary containing four QuantumCircuit objects which prepare the two-qubit system in different initial states
Args:
q (QuantumRegister): the register to use for the circuit
system (list): list of indices for the system qubits
Returns:
A dictionary with the initial state QuantumCircuit objects and a list of labels
"""
# State labels
state_labels = ['00', '01', '10', '11']
ic = {}
for ic_label in state_labels:
ic[ic_label] = QuantumCircuit(q)
# |01>
ic['01'].x(q[system[0]])
# |10>
ic['10'].x(q[system[1]])
# |11>
ic['11'].x(q[system[0]])
ic['11'].x(q[system[1]])
return ic, state_labels
SHOTS = 8192
# The values for p
p_values = np.linspace(0, 1, 10)
# We create the quantum circuits
q = QuantumRegister(5, name='q')
c = ClassicalRegister(2, name='c')
## Index of the system qubit
system = [2, 1]
## Indices of the ancillary qubits
a_zz = 0
a_xx = 4
## Prepare the qubits in four initial conditions
ic_circs, ic_state_labels = initial_conditions(q, system)
## Three different channels, each with
## four initial conditions and ten values of p
pumps = ['ZZ', 'XX', 'ZZ_XX']
circuits = {}
for pump in pumps:
circuits[pump] = {}
for ic in ic_state_labels:
circuits[pump][ic] = []
for ic in ic_state_labels:
for p in p_values:
circuits['ZZ'][ic].append(ic_circs[ic]+zz_pump(q, c, p, system, a_zz))
circuits['XX'][ic].append(ic_circs[ic]+xx_pump(q, c, p, system, a_xx))
circuits['ZZ_XX'][ic].append(ic_circs[ic]+zz_xx_pump(q, c, p, system, [a_zz, a_xx]))
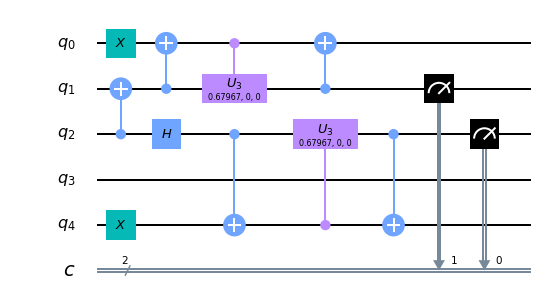
circuits['ZZ_XX']['00'][1].draw(output='mpl')
# Execute the circuits on the local simulator
jobs_sim = {}
for pump in pumps:
jobs_sim[pump] = {}
for ic in ic_state_labels:
jobs_sim[pump][ic] = execute(circuits[pump][ic], backend = simulator, shots = SHOTS)
# Analyse the outcomes
overlaps_sim = {}
for pump in pumps:
overlaps_sim[pump] = {}
for ic in ic_state_labels:
overlaps_sim[pump][ic] = [0.0]*len(p_values)
for i in range(len(p_values)):
for ic in ic_state_labels:
counts = jobs_sim[pump][ic].result().get_counts(i)
for outcome in counts:
overlaps_sim[pump][outcome][i] += counts[outcome]/(4.0 * float(SHOTS))
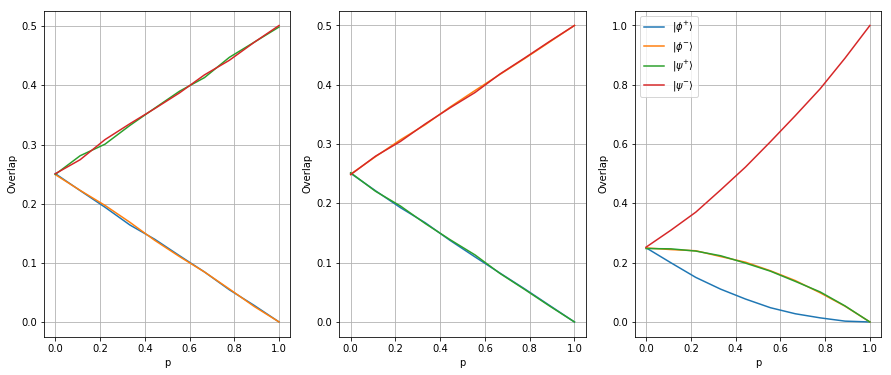
# Plot the results
fig_idx = 131
plt.figure(figsize=(15,6))
bell_labels = {'00': r"$| \phi^{+} \rangle$", '01': r"$| \phi^{-} \rangle$", '10': r"$| \psi^{+} \rangle$", '11': r"$| \psi^{-} \rangle$"}
for pump in pumps:
plt.subplot(fig_idx)
for outcome in overlaps_sim[pump]:
plt.plot(p_values, overlaps_sim[pump][outcome], label = bell_labels[outcome])
plt.xlabel('p')
plt.ylabel('Overlap')
fig_idx += 1
plt.grid()
plt.legend();
# Calibration circuits
cal_circuits, state_labels = complete_meas_cal(system, q, c)
# Run the calibration job
calibration_job = execute(cal_circuits, backend, shots=SHOTS)
# Run the circuits and save the jobs
jobs = {}
jobs_data = []
for pump in pumps:
jobs[pump] = {}
for ic in ic_state_labels:
jobs[pump][ic] = execute(circuits[pump][ic], backend = backend, shots = SHOTS)
# Use the calibration job to implement the error mitigation
meas_fitter = CompleteMeasFitter(calibration_job.result(), ic_state_labels)
meas_filter = meas_fitter.filter
overlaps = {}
for pump in pumps:
overlaps[pump] = {}
for ic in ic_state_labels:
overlaps[pump][ic] = [0.0]*len(p_values)
for i in range(len(p_values)):
for ic in ic_state_labels:
counts = meas_filter.apply(jobs[pump][ic].result()).get_counts(i)
for outcome in counts:
overlaps[pump][outcome][i] += counts[outcome]/(4 * float(SHOTS))
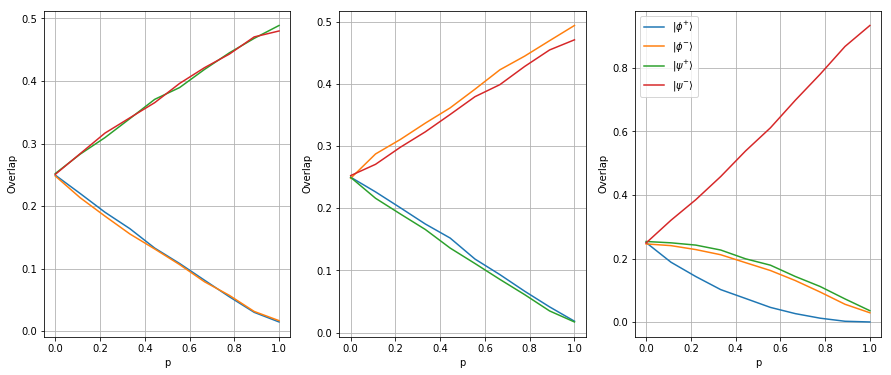
# Plot the results
fig_idx = 131
plt.figure(figsize=(15,6))
bell_labels = {'00': r"$| \phi^{+} \rangle$", '01': r"$| \phi^{-} \rangle$", '10': r"$| \psi^{+} \rangle$", '11': r"$| \psi^{-} \rangle$"}
for pump in pumps:
plt.subplot(fig_idx)
for outcome in overlaps[pump]:
plt.plot(p_values, overlaps[pump][outcome], label = bell_labels[outcome])
plt.xlabel('p')
plt.ylabel('Overlap')
fig_idx += 1
plt.grid()
plt.legend();